Mustererkennung auf Patientendaten: Teil 2

12. Juli 2022

Nach der methodischen Einführung der Mustererkennung möchten wir im zweiten Teil – inspiriert durch Daniel Jurafsky und James H. Martin im Buch „Speech and Language Processing (https://web.stanford.edu/~jurafsky/slp3/)“ – anhand einer sehr einfachen Methodik, dem Naive-Bayes-Klassifikator, das Prinzip der Empfehlungen mit Erklärungen erläutern. Der Naive-Bayes-Klassifikator zählt innerhalb der Trainingsdaten, wie häufig ein ICD-Code mit anderen ICD-Codes auftritt. Anschließend nutzt er den Satz von Bayes, um die bedingte Wahrscheinlichkeit umzuformulieren:

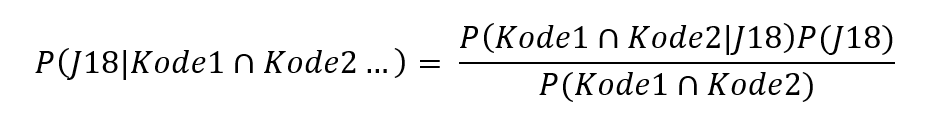
Nehmen wir nun vereinfacht an, dass alle Kodes unabhängig voneinander sind, können wir weiter umformulieren:

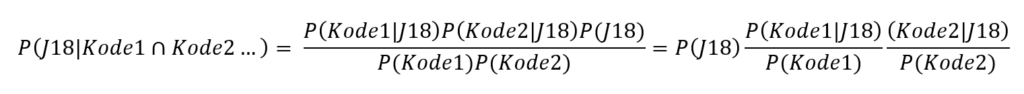
Somit benötigen wir für das Abschätzen der Wahrscheinlichkeit für das Kodieren des abhängigen Kodes J18 nur die Grundwahrscheinlichkeit von J18 sowie die Likelihoods und Grundwahrscheinlichkeiten der unabhängigen Kodes Kode1, Kode2.

Dazu benötigen wir zunächst die das Verhältnis der Patientenfälle, mit der ein ICD-Code (z. B. J91) auftritt, über die Grundgesamtheit aller Patientenfälle. Diese Wahrscheinlichkeit nennen wir Grundwahrscheinlichkeit der ICD-Codes (bzw. mathematisch A-priori-Wahrscheinlichkeit), da sie die Anfangswahrscheinlichkeit eines ICD-Codes in der Grundgesamtheit der Patientenfälle widerspiegelt. Berechnen lässt sich diese A-priori-Wahrscheinlichkeit durch:

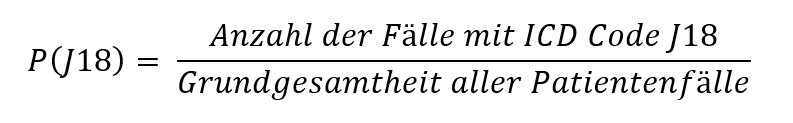
Als nächsten Schritt werden die Likelihoods der ICD-Codes berechnet. Unter der Likelihood der ICD-Codes verstehen wir die bedingte Wahrscheinlichkeit, dass ein ICD-Code, in Verbindung mit dem Target-ICD-Code in der Abrechnung eines Patientenfalls vorkommt. Wir beantworten mit der Berechnung der Likelihoods der ICD-Codes die Frage:

Wie wahrscheinlich tritt ein bestimmter ICD-Code auf, wenn bei einem Patientenfall bereits der Target-ICD-Code annotiert wurde?

Um diese Likelihoods zu berechnen, zählen wir zunächst in unserer Grundgesamtheit die Anzahl der Patientenfälle, in denen der ICD-Code J91 gemeinsam mit dem Target-ICD-Code vorkommt, und teilen diese Zahl durch die Anzahl an Patientenfälle mit abgerechnetem Target-ICD-Code (also True Class-Patientenfälle). Mathematisch können wir diese Likelihood so ausdrücken:

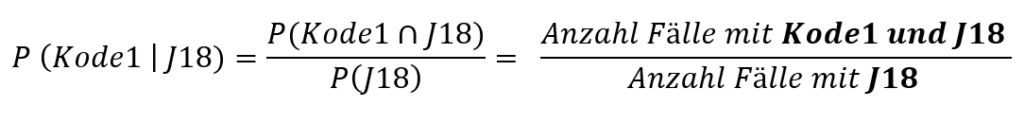
Um die vorhergesagten Ergebnisse des maschinellen Lernverfahrens besser nachvollziehen und vergleichen zu können, nutzen wir nun das Prinzip des Satzes von Bayes, um mithilfe bedingter Wahrscheinlichkeiten (Likelihoods) und den Grundwahrscheinlichkeiten aller ICD-Codes einen Erklärbarkeits-Indikator zu berechnen.

Dazu teilen wir die Likelihoods der ICD-Codes durch die Grundwahrscheinlichkeiten der ICD-Codes:

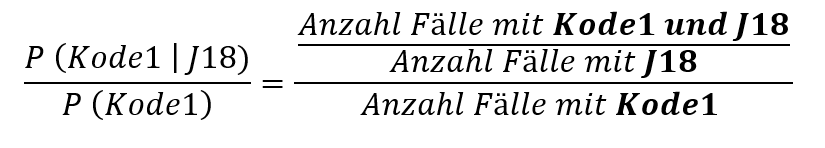
Wir verstehen dieses Wahrscheinlichkeitsverhältnis als einen Indikator, ob ein ICD-Code unseren Target-ICD-Code womöglich gut oder schlecht „erklären“ kann, wie auch in der folgenden Tabelle beschrieben:

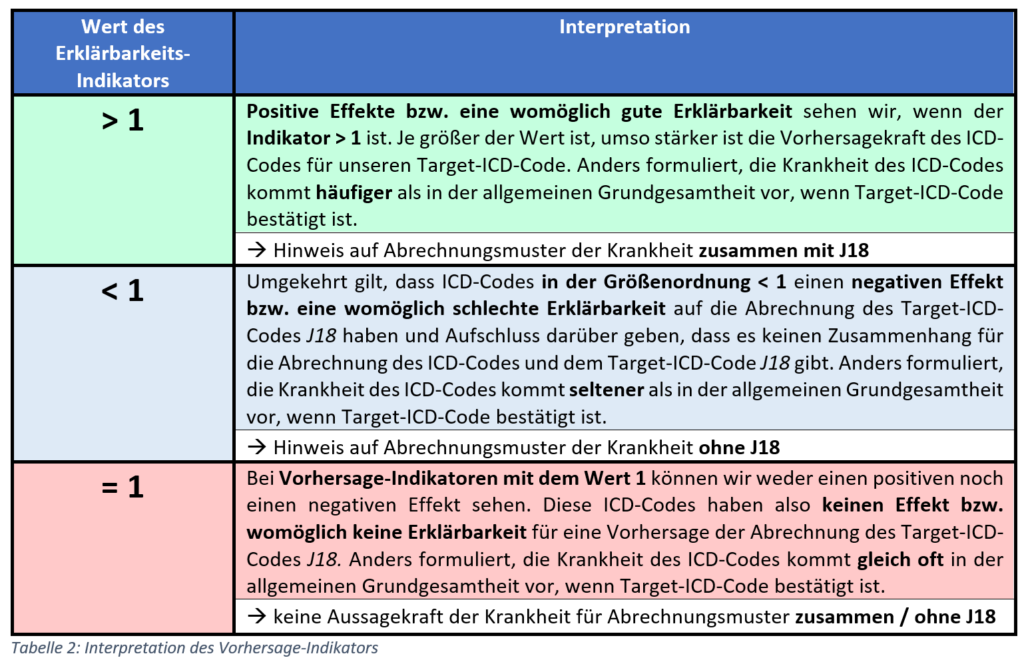
Natürlich kann ein Code auch aus Zufall oder aufgrund von Nebeneffekten einen besonders hohen oder niedrigen Erklärbarkeits-Indikator aufweisen. Daher sollte er auf einer möglichst hohen Menge an Daten berechnet werden. Außerdem sollte er aus klinischer Perspektive auf Plausibilität evaluiert werden.

Anschließend können wir für beliebige Patientenfälle die Wahrscheinlichkeit für das zusätzliche Kodieren eines Codes annähernd berechnen, indem wir die Apriori-Wahrscheinlichkeit des Kodes mit den Vorhersage-Indikatoren aller anderen Kodes multiplizieren:

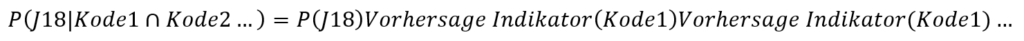
Es handelt sich hier nur um eine Abschätzung, denn der Naive-Bayes nimmt hierbei vereinfachend an, dass alle ICD-Kodes voneinander unabhängig sind, was sie allerdings sicherlich (und gewollter Weise) nicht sind. Allerdings stellt es eine einfach verständliche und effiziente Möglichkeit zu Berechnung und Anwendung von Mustern auf Patientendaten dar.

Beispielhafte Ergebnisse

Im Folgenden zeigen wir Beispiele für Grundwahrscheinlichkeiten, Likelihoods und Erklärungs-Indikatoren.

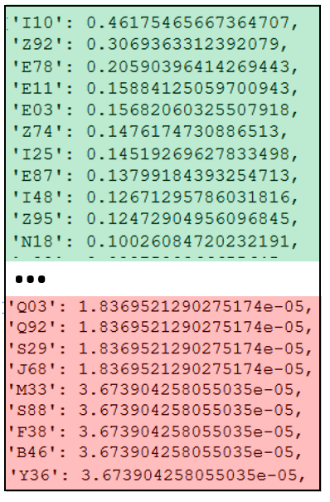
Abb. 3 zeigt eine mögliche sortierte Auflistung von Grundwahrscheinlichkeiten; so im grünen Bereich, dass ICD-Codes wie I10.- (Essentielle (primäre) Hypertonie) mit 46%, Z92.- (Medizinische Behandlung in der Eigenanamnese) mit 30% oder E78 (Störungen des Lipoproteinstoffwechsels und sonstige Lipidämien) mit 20% besonders häufig in Patientenfällen abgerechnet werden.

Ebenso sehen wir eher unterrepräsentierte ICD-Codes im roten Bereich, d.h. ICD-Codes wie etwa Q03.- (Angeborener Hydrozephalus) mit A-Priori-Wahrscheinlichkeiten von 0.00183%, S88.- (Traumatische Amputation am Unterschenkel) oder Y36.- (Verletzungen durch Kriegshandlungen) mit jeweils 0.00367% treten sehr selten in Patientenfällen auf

Als Likelihoods können sich zum Beispiel ergeben, dass insbesondere die ICD-Codes I10 mit63 %, Z92 mit 51 % oder E87.- mit 43 %die größten Likelihoods zum Target-Kode J18 haben.

In der Form von daraus berechneten Vorhersage-Indikatoren können wir somit nützliche und erklärbare Muster bzgl. der J18-Pneumonie erkennen. Diese Muster können auf Plausibilität evaluiert und zur Entscheidungsunterstützung der Kodierung in ein klinisches Abrechnungssystem eingespeichert werden. Auch dies wollen wir im Folgenden beispielhaft zeigen. Dazu betrachten wir nur Muster bzw. Regeln, die einen ausreichenden Support haben, d. h. auf einer Mindestanzahl an Patientenfällen gezeigt werden konnte.

Im Folgenden zwei medizinisch naheliegende Muster, die für eine J18-Kodierung sprechen:

J91 à J18: Pleuraerguss J91.- erklärt Pneumonie J18.-

Die Take-Home-Message

In der Praxis bedeuten gelernte Muster – übersetzt in den Arbeitsalltag eines Medizincontrollers oder einer Kodierfachkraft – Qualitätssicherung und Wissensgenerierung über Patientendaten: Wenn Kodierfachkräfte wissen, welche ICD-Datenmuster bei Krankheitsfällen existieren, fällt es ihnen womöglich leichter, solche Datenmuster bei der Kodierung stärker zu berücksichtigen und damit die Gefahr von Inkonsistenzen der Kodierung zu minimieren. Sollten Datenmuster sich als universal anwendbar herausstellen, könnten im Idealfall aus der statistischen Erfahrung Kodierregeln erzeugt werden, welche aufgrund der erkannten Datenmuster bei bestimmten ICD-Codes eine Entscheidungsunterstützung durch KI-gestützte Abrechnungskodierung für Kodierfachkräfte bieten.

Drei Aspekte verdienen hierbei besondere Beachtung:

Das Häufige ist häufig, das Seltene ist selten: Aus der Vergangenheit zu lernen ist sehr wichtig. Gleichzeitig sollte man nicht vergessen, dass man hier mit Unschärfen arbeitet. Weder sollte man bei kleinsten Anzeichen direkt auf die unwahrscheinlichsten Diagnosen und Kodierungen schließen (Zebras – https://flexikon.doccheck.com/de/Zebra), noch sollte man die Möglichkeit ignorieren, dass eine seltene (dafür ggf. einflussreiche) Situation tatsächlich eingetreten ist. Ein Kompromiss zwischen Aufwand und Mehrwert muss in jedem Anwendungsfall individuell gefunden werden.

Unabdingbar ist eine hohe Erklärbarkeit der Entscheidungsunterstützung: Das Problem vieler Maschineller-Lernverfahren ist ihre begrenzte Erklärbarkeit. Je höher die Erklärbarkeit, z.B. erreicht durch Methoden der „Explainable Artificial Intelligence (XAI)“ (Paper: https://doi.org/10.1016/j.inffus.2019.12.012), desto höher häufig der Mehrwert und die Akzeptanz der Nutzer. Hierzu ist meist eine Feedback-Schleife notwendig, um globale oder lokale Muster auf medizinische Plausibilität zu testen und das System gezielt zu trainieren.

Je mehr Daten, desto mehr Möglichkeiten: Wir haben in diesem Blogartikel nur Abrechnungsdaten analysiert; es bestand also eine begrenzte Informationsgrundlage. Je höher die Informationsgrundlage, desto höher häufig der Mehrwert. Die Ansätze lassen sich jedoch genauso auch bei größerer Informationsgrundlage anwenden. Mit dem Datenumfang nehmen Laufzeit der Algorithmen und der Aufwand bei der Datenvorverarbeitung zu, z.B. wenn es sich bei der klinischen Dokumentation um longitudinale Labordaten oder unstrukturierte Freitextdokumente handelt. Das gezeigte Prinzip lässt sich selbstverständlich auch für eine klinische Entscheidungsunterstützung nutzen, allerdings mit vielfach höheren Anforderungen an Mehrwert und Akzeptanz der Nutzer.

So lässt sich abschließend sagen, es lohnt sich sicher, nützliche Muster auf medizinischen Daten automatisiert zu erkennen. Wie hoch der Mehrwert im Vergleich zum Aufwand ausfällt, kommt auf den Anwendungsfall an sowie, ob bereits Modelle aus vorhergehenden Projekten vorhanden sind.

Vielen Dank an Benedikt Kämpgen, Nico Hermeling, Tobias Stening und Anastasia Ribatschok für die Mithilfe bei diesem Blogartikel.

Lukas Probst ist Praktikant im Team „Healthcare Analytics“ bei Empolis. In seinem Praktikum beschäftigt sich Lukas mit Data Science im Gesundheitswesen und untersucht, welche Muster man in den Abrechnungsdaten von Krankenhäusern beobachten kann. Hierbei hilft ihm seine Affinität und Interesse an mathematischen Fragestellungen, die er bereits in seinem Studium des Wirtschaftsingenieurwesens an der Technischen Hochschule Ingolstadt entdeckt hat. Während des Studiums hat Lukas bereits Erfahrungen in Kundenprojekten im Schwerpunkt Kostenoptimierung und -analyse als Dualer Student einer technischen Unternehmensberatung gesammelt. In seiner Freizeit versucht Lukas möglichst viel Teamsportarten zu machen und liest gerne englischsprachige Bücher oder (Fach-)Artikel.